Cours de maths de 6ème

Des cours gratuits de mathématiques de niveau collège pour apprendre réviser et approfondir
Des exercices et sujets corrigés pour s'entrainer.
Des liens pour découvrir

Cours de maths 6eme

Cours sur les figures planes

Les triangles

Les triangles

Objetcifs du cours:
- Connaître la définition d'un triangle
- Connaître les éléments caractéristiques d'un triangle ( cotés, sommets et angles )
- Savoir tracer un triangle
- Connaître les triangles particuliers ( isocèle, équilatéral et rectangle ) ainsi que leurs propriétés

Qu'est ce qu'un triangle ?
Par définition un triangle est une figure qui possède 3 cotés.
Par conséquent un triangle possède également trois sommets et trois angles
Exemple:

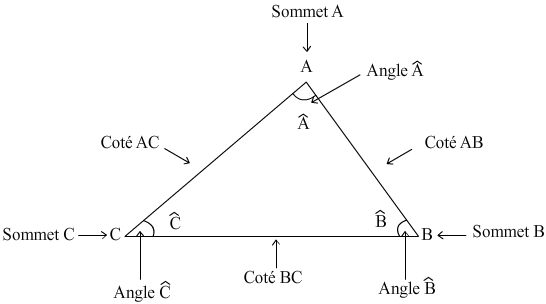
Tracer un triangle
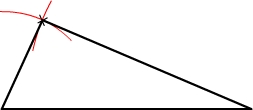
Tracer un triangle ABC:
- On commence de tracer à la règle le segment AB

- On trace en suite un arc de cercle à l'aide d'un compas centré en A et en lui donnant une ouverture correspondant à la longueur du segment AC.

- On trace un deuxième arc de cercle à l'aide d'un compas centré en B dont l'ouverture correspond à la longueur du segment BC

- L'intersection des deux arcs de cercle correspond au sommet C. Il suffit de alors de tracer AC et BC en joignant ces points.

Les triangles particuliers
Il existe plusieurs cas particuliers de triangles:
- Le triangle isocèle est un triangle qui possède deux cotés de même longueur.

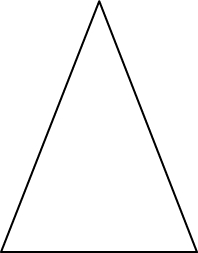
- Le triangle équilatéral est un triangle dont tout les cotés ont même longueur.

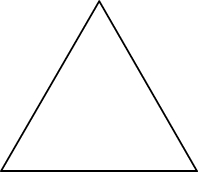
- Le triangle rectangle est un triangle dont dont un des angles est un angle droit ( 90° )

D'autres cours, exercices, documents et activités en liaison avec les triangles
Cours de 5eme sur l'aire d'un triangle
Cours de 4eme: théorème de Pythagore dans un triangle rectangle
Cours sur les triangles
Cours sur les triangles isocèles
Cours sur les triangles rectangles
Cours: Tracer un triangle est ses éléments caractéristiques